О некоторых особенностях расчета стандартных мер емкости остродонных амфор
с.106 Известно, что амфоры античных центров являлись стандартной тарой, причем каждая мера емкости имела строго обусловленные линейные размеры1. В то же время оставалось неясно, каким образом греки рассчитывали эти меры емкости. В результате многолетних исследований было высказано предположение, что амфорные стандарты емкости могли рассчитываться по одной или нескольким формулам, известным как формулы Герона.
Наибольшие успехи в изучении античной метрологии и особенно стандартов емкости достигнуты
Вместе с тем
с.107 На этом основании был сделан вывод о существовании в античности каких-то не дошедших до нас формул расчета объема тел вращения, которые, скорее всего, создавались для каждого типа сосудов экспериментально. М. Лэнг даже предложила одну формулу (11/14×(¾макс. диам.)2×глубина) для вычисления объема панафинейских амфор. Впрочем, применить ее к остродонным амфорам оказалось невозможным3.
Наши исследования херсонесской тары в целом подтверждают выводы
Стандартные меры емкости амфор объемом в 3—
В то же время нельзя быть полностью уверенным в том, что расчет этих мер производился именно по формулам Герона, а не по каким-то другим неизвестным нам формулам. Кстати сказать, в источнике совершенно определенно говорится о применимости формул Герона только для пифосов, а выбор той или иной из них ставится в зависимость от формы сосуда («пифоид», «сфероидный пифос» и «другой пифос»)5. Тот факт, что две первые формулы подходят для всех херсонесских и некоторых средиземноморских и южнопонтийских амфор, может оказаться случайным совпадением. Весьма вероятно, что настоящий расчет стандартов производился иначе.
с.108 Для реконструкции этой методики, прежде всего, видимо, следует детально расшифровать уже известные нам формулы Герона. Так, уже отмечалось, что коэффициенты 11/14 и 11/21 являются хорошим приближением к дробным частям числа π: 11/14=π/4, а 11/21=π/66. В преобразованном виде обе формулы выглядят следующим образом: π/4 (или π/6)×Dср.2×H0, где Dср. (средний диаметр) есть половина суммы наибольшего диаметра тулова и диаметра устья. В таком случае формула Герона с коэффициентом 11/14 является формулой объема цилиндра, у которого диаметр основания равен среднему диаметру (D+d)÷2, а высота — глубине амфор конкретной меры емкости (рис. 1). Другими словами, наблюдается равенство π/4×Dср.2×H0=π×r2×H0.
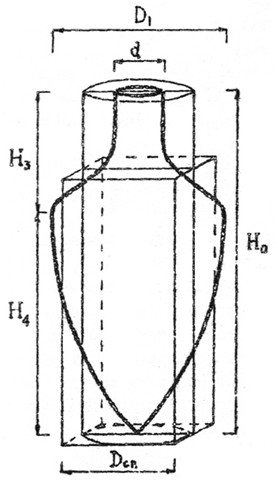
Рис. 1. Пространственная схема героновской формулы «пифоида» и новой формулы расчета емкости амфор «пифоидного типа» |
Вторая формула Герона — «сфероидного пифоса» — где используется коэффициент 11/21 (или π/6), аналогичным образом преобразуется в современную формулу объема конуса. Диаметр основания этого конуса будет равен Dср., а высота — 2×H0.
Выявленные закономерности заставили более тщательно проанализировать линейные размеры керамической тары Херсонеса и особенно соотношения этих размеров. Так, при обработке среднеарифметических значений линейных размеров амфор емкостью в 2—
Если формула «пифоида» определяет объем цилиндра, у которого диаметр основания равен Dср., а высота — глубине амфор данной меры емкости, то согласно новой формуле мы получаем совершенно иную пространственную фигуру — параллелепипед, у которого сторона основания равна Dср., а высота — 11/14 глубины амфоры или разнице между глубиной и высотой горла (рис. 1). Отметим, что основание цилиндра (формула Герона) оказывается кругом, вписанным в квадрат, являющийся основанием параллелепипеда.
Данное равенство объемов двух фигур расшифровывается в соответствии с одной из теорем, приписываемых Архимеду, и сформулированной следующим образом: круг к квадрату на диаметре относится как 11 к 147. Иначе, площадь круга, вписанного в квадрат, составляет 11/14 от площади данного квадрата. Из теоремы следует, что для равенства объемов цилиндра и параллелепипеда высота второго должна составлять 11/14 высоты цилиндра. Это мы и наблюдаем в данном случае.
Реконструированная формула H4×Dср.2, на наш взгляд, более удобна, чем соответствующая формула Герона. Кроме несомненной простоты в ее пользу свидетельствует явная закономерность — реальная емкость амфор всегда несколько больше стандартной меры, судя по всему, с расчетом на объем, занимаемый пробкой, необходимой воздушной прослойкой между содержимым и пробкой и
Что же касается херсонесских амфор малых мер емкости (3 и 4 хойника), то для них выявлена другая закономерность. В данном случае произведение фактической глубины на коэффициент 11/21 равно разности между глубиной и высотой верхней части сосуда: 11/21×H0=H0—
Обе реконструированные формулы проще, удобнее и логически более оправданы. На херсонесском материале их предпочтительность вряд ли вызовет сомнения, однако для полной убедительности нужна проверка на амфорах других центров.
В нашем распоряжении, к сожалению, не оказалось измерений емкости и линейных параметров амфор хотя бы нескольких античных центров — экспортеров вина и оливкового масла. Поэтому, кроме херсонесских сосудов была использована только одна фасосская амфора из Нимфея, изданию которой
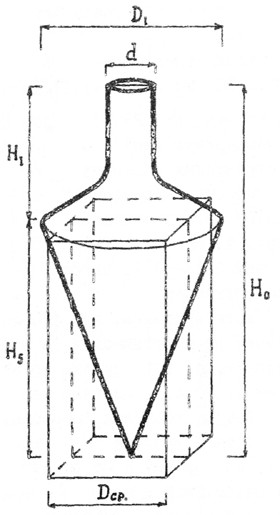
Рис. 2. Пространственная схема новой формулы расчета емкости амфор вытянутой формы |
Вызывают сомнения два момента. Во-первых, вероятная стандартная мера равна или даже больше фактической емкости, чего не должно было бы наблюдаться13. Во-вторых, очень неудобные цифры получены для размеров D и d, сумма которых дает нечетное число. Следовательно, средний диаметр, который фактически используется при вычислении меры, выражен дробным числом (21+6)÷2=13.5 дактиля. Если первое замечание можно объяснить неточностью в производстве сосуда, то второй момент такого объяснения не находит.
Нам кажется, что в данном случае, как и у херсонесских амфор, в качестве наибольшего диаметра должен браться не внешний, а внутренний диаметр тулова (без толщины стенок — D1), который в таком случае равен 20 ионийским дактилям. Тогда средний диаметр будет равен целому числу (20+6)÷2=13. Недоумения этот факт не должен вызывать. В конечном счете гончар, на практике зная с.112 возможную усадку изделия при сушке и обжиге14, мог с одинаковым успехом запланировать как внешний, так и внутренний диаметр тулова.
Если теперь повторить расчет по формуле Герона с учетом D1=20, мы получим: 11/14×[(20+6)÷2]2×28=3718 ионийских куб. дактилей, или 23.54 литра. В таком случае эта амфора вмещала стандартную меру в 8 фасосских хоев (в 2.94 литра)15, или в метрических единицах 23.52 литра, фактическое совпадение теоретически рассчитанной меры и содержания стандарта (23.54 и 23.52 литра) выглядит довольно убедительно. Остаток объема от полной емкости (25.7 литра) до стандарта, таким образом, составит 2.16—
Если признать, что фасосская амфора из Нимфея имеет меру емкости не в аттических, а в фасосских хоях, то, следовательно, или амфора изготовлена до введения в действие закона Клеарха 449 г. до н. э. об унификации мер и весов, или этот афинский декрет не коснулся фасосских мер емкости.
Хотя в публикации не приведена высота горла фасосской амфоры, по чертежу этот размер довольно надежно восстанавливается и равен, скорее всего, 6 ионийским дактилям. Таким образом, размер H4 для реконструированной формулы определяется как (28—
В итоге можно отметить, что две реконструированные формулы могли быть использованы для расчета стандартных мер емкости античных остродонных амфор. Их преимущество по сравнению с дошедшими до нас формулами Герона состоит как в простоте вычислений, так и в иной принципиальной основе. Употребление этих формул не связано с числом π, а опиралось на равенство объемов параллелепипеда и сложнопрофильной сфероидной фигуры (амфоры), причем необходимая высота теоретического параллелепипеда для каждого типа сосудов определялась отдельно и, видимо, экспериментально.
с.113
| № п/п | Стандартная мера емкости | Система линейных измерений | Дактильные размеры в дактилях | Формула Герона | Результат вычисления по формуле Герона | Новая формула | Результат вычисления по новой формуле | ||||||||||
| хойников | гемигектов | литров | H0 | D1 | d | H1 | H3 | H4 | H5 | куб. дакт. | литр | куб. дакт. | литр | ||||
| 1 | 3[1] | — |
3.28 | аттич. | 20 | 9 | 3 | 9 | — |
— |
11 | 11/21×H0× [(D+d)÷2]2 |
377 | 3.21 | H5× Dср.2 |
396 | 3.37 |
| 2 | 4[1] | 1 | 4.37 | « | 26 | 9 | 4 | 13 | — |
— |
13 | « | 575 | 4.89 | « | 549 | 4.67 |
| 3 | 4 | 1 | 4.37 | « | 22 | 10 | 3 | 10 | — |
— |
12 | « | 486 | 4.13 | « | 506 | 4.31 |
| 4 | 8 | 2 | 8.75 | « | 26 | 10 | 4 | — |
5 | 21 | — |
11/14×H0× [(D+d)÷2]2 |
1000 | 8.46 | H4× Dср.2 |
1029 | 8.75 |
| 5 | 12 | 3 | 13.13 | « | 32 | 12 | 4 | — |
8 | 24 | — |
« | 1607 | 13.66 | « | 1600 | 13.60 |
| 6 | 16 | 4 | 17.51 | « | 32 | 14 | 4 | — |
7 | 25 | — |
« | 2036 | 17.31 | « | 2025 | 17.21 |
| 7 | 20 | 5 | 21.89 | « | 32 | 16 | 4 | — |
7 | 25 | — |
« | 2514 | 21.26 | « | 2500 | 21.25 |
| 8 | 24 | 6 | 26.26 | « | 32 | 17 | 5 | — |
7 | 25 | — |
« | 3042 | 25.85 | « | 3025 | 25.71 |
| 9 | 24 | 6 | 26.26 | ионийск. | 36 | 19 | 5 | — |
8 | 28 | — |
« | 4073 | 25.78 | « | 4032 | 25.52 |
с.114 Полученные на основе анализа метрологических характеристик античных амфор результаты позволяют утверждать, что приписываемая Архимеду теорема о соотношении площадей круга и квадрата, построенного на диаметре, была известна и использовалась греками в практической деятельности, по крайней мере, уже в
Фактическое совпадение результатов вычисления по формулам Герона и реконструированным формулам на основе херсонесского амфорного материала не означает, что такое явление должно наблюдаться во всех случаях. Весьма вероятно, что отдельные группы тары не будут просчитываться по формулам Герона, но дадут удовлетворительный результат по реконструированным формулам. Несомненно, что подобных формул расчета стандартных мер емкости амфор существовало несколько.
ПРИМЕЧАНИЯ